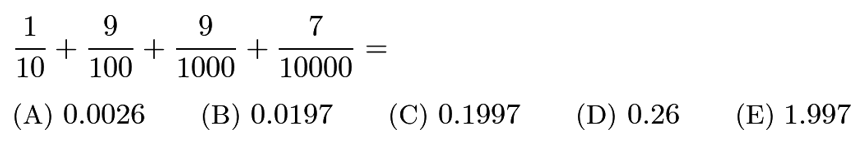
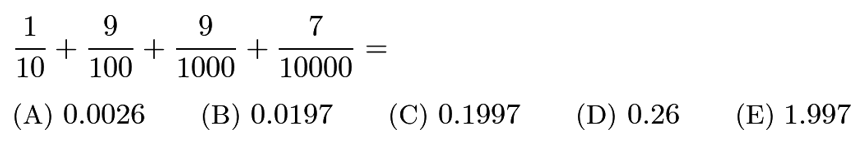
Answer: C
Solution:
=0.1+0.09+0.009+0.0007=0.1997.

Answer: D
Solution:
The smallest two-digit integer he can subtract from 200 is 10. This will give the largest result for that first operation, and doubling it will keep it as the largest number possible. 200-10=190, 190*2=380.
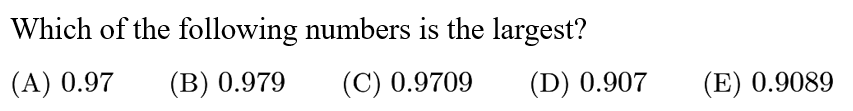
Answer: B
Solution:
0.979 is the largest

Answer: E
Solution:
30*150~45*150 =>4500~6750.

Answer: A
Solution:
Writing out all the two digit multiples of 7, you get 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98. Again you find 28 , 91 have a digital sum of 10 , giving answer A.
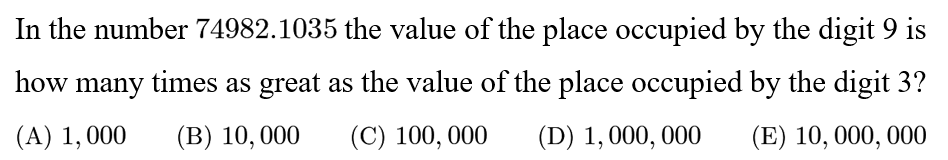
Answer: C
Solution:
The digit 9 is 5 places to the left of the digit 3. Thus, it has a place value that is 10^5=100,000.

Answer: D
Solution:
Draw a square circumscribed around the circle. (Alternately, the circle is inscribed in the square.) If the circle has radius 4, it has diameter 8. the smallest square that contains it has side length 8, and area 8*8=64.

Answer: B
Solution:
There are 8+1/2 hours (510 minutes) from 7:30 a.m. to 4 p.m. Tallying up the times he was not on the bus, he has 6*50=300 minutes in classes, 30 minutes at lunch, 2*60=120 minutes of "additional time". That is a total of 300+30+120=450 minutes that Walter was away from home, but not on the bus. Therefore, Walter spent 510-450=60 minutes on the bus.

Answer: C
Solution:
There are 3 ways to pick the first student, 2 ways to pick the second student, and 1 way to pick the last student, for a total of 3*2*1=6 ways to line the students up. Only 1 of those ways is alphabetical. Thus, the probability is 1/6.

Answer: C
Solution:
Fill in grid lines to make the shape look like a small 6x6 checkerboard.
There are 6*6 squares total. Instead of counting shaded squares, count unshaded squares. There are 1+5+9=15 unshaded squares. Thus 36-15=21 of the square is shaded, it is 21/36=7/12.

Answer: A
Solution:
11 has 2 factors, and 20 has 6 factors; 2*6=12; 12 has 6 factors ,so the answer is 6.
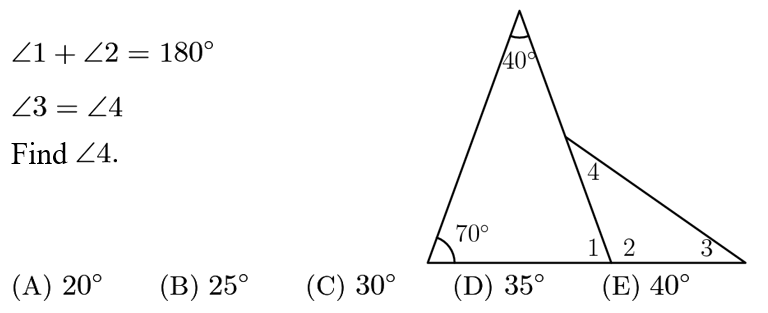
Answer: D
Solution:
<1=180-40-70=70; <2=180-<1=180-70=110;
<3+<4+<2=180, so <3+<4=180-110=70; because <3=<4, so <4=70/2=35.

Answer: A
Solution:
In bag A, there are 26*50%=13 yellow beans.
In bag B, there are 28*25%=7 yellow beans.
In bag C, there are 30*20%=6 yellow beans.
Totally, the ratio yellow beans is : (13+7+6)/(26+28+30)=30.9%.

Answer: D
Solution:
When these numbers are ordered in ascending order, 5, the median, falls right in the middle, which is the third integer from the left. Since there is a unique mode of 8, both integers to the right of 5 must be 8s. Since the mean is 5, the sum of the integers is 25, which means the 2 leftmost integers have to sum to 4. 2 and 2 does not work because that would result in two modes. However, 1 and 3 does, and so our answer is 8-1=7.
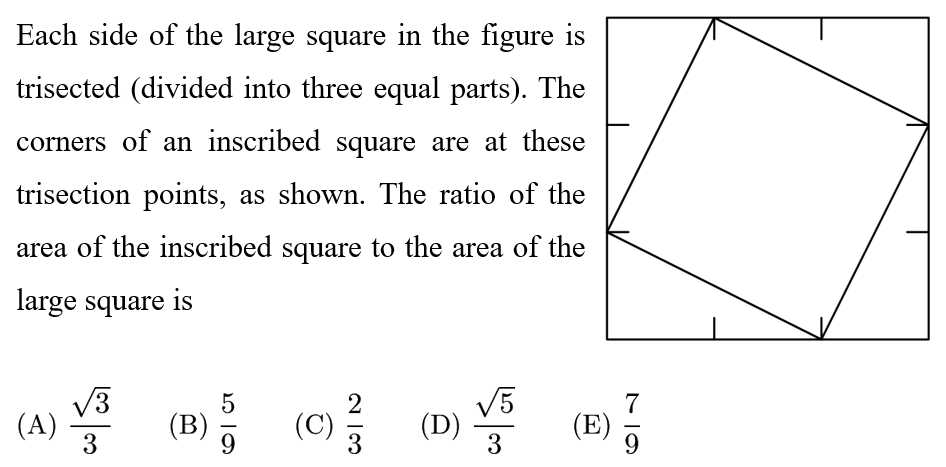
Answer: B
Solution:
Since we are dealing with ratios, let the big square have sides of 3 and thus an area of 3*3=9. To find the area of the inscribed square, subtract off the areas of the four triangles. Each triangle has an area of 1/2*1*2=1. Thus, the area of the inscribed square is 9-4*1=5, and the ratio of areas is 5/9.

Answer: E
Solution:
AA: 100*1.2*0.8=0.96;
BB: 100*0.75*1.25=0.94;
Cc: 1. Thus, B<A<C.
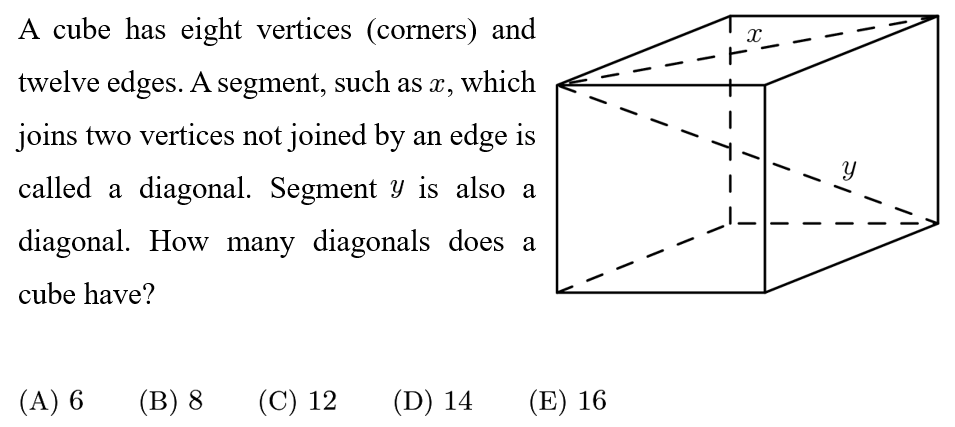
Answer: E
Solution:
On each face, there are 2 diagonals like x. There are 6 faces on a cube. Thus, there are 2*6=12 diagonals that are "x-like".
Every "y-like" diagonal must connect the bottom of the cube to the top of the cube. Thus, for each of the 4 bottom vertices of the cube, there is a different "y-like" diagonal. So there are 4 "y-like" diagonals. This gives a total of 12+4=16 diagonals on the cube.

Answer: B
Solution:
Last week, each box was 5/4. This week, each box is 4/5.
Percent decrease is given by (5/4-4/5)/(5/4)=36%.
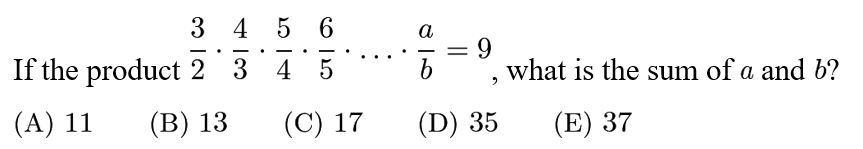
Answer: D
Solution:
Notice that the numerator of the first fraction cancels out the denominator of the second fraction, and the numerator of the second fraction cancels out the denominator of the third fraction, and so on.
The only numbers left will be a in the numerator from the last fraction and 2 in the denominator from the first fraction. Thus, a/2=9, => a=18. Since the numerator is always one more than the denominator, b=a-1=17. a+b=35.

Answer: A
Solution:
Make a chart with all products. 10 work out of 64. Simplify for 5/32.
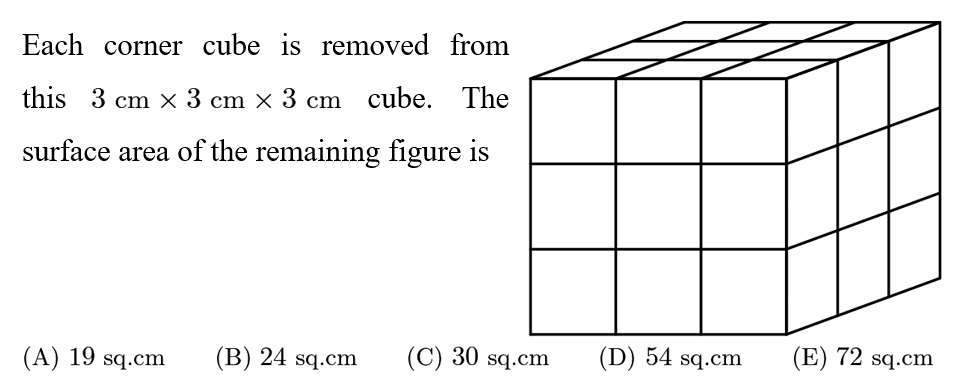
Answer: D
Solution:
The original cube has 6 square surfaces that each have an area of 3*3=9, for a total surface area of 6*9=54. Since no two corner cubes touch, we can examine the effect of removing each corner cube individually.
Each corner cube contribues 3 faces each of surface area 1 to the big cube, so the surface area is decreased by 3 when the cube is removed. However, when the cube is removed, 3 faces on the 3x3x3 cube will be revealed, increasing the surface area by 3.
Thus, the surface area does not change with the removal of a corner cube, and it remains 54.
Answer: E
Solution:
The 2x2x2 cube of silver can be divided into 8 equal cubes that are 1x1x1. Each smaller cube is worth 200/8=25 dollars.
To create a 3x3x3 cube of silver, you need 27 of those 1x1x1 cubes. The cost of those 27 cubes is 27*25=675 dollars.
Method 2: (2*2*2)/200=(3*3*3)/x ; => x=675.

Answer: C
Solution:
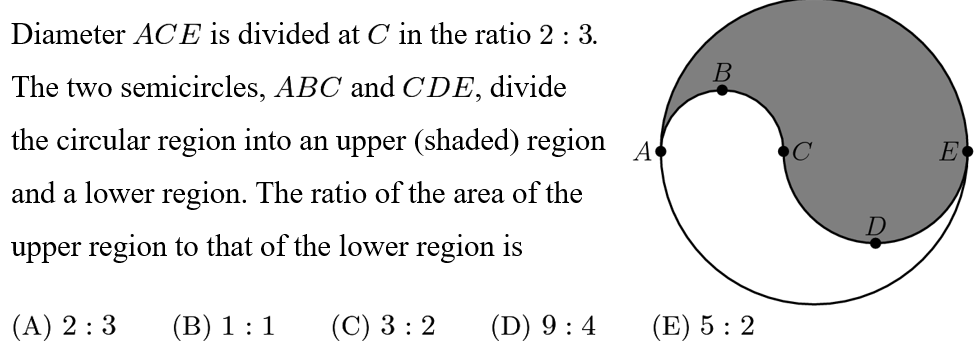
Answer: C
Solution:
Draw AE to divide the big circle in half. Assign AC=4, CE=6 so that the radii work out to be integers. The shaded region is equal to the area of semicircle AE on top, plus the area of the semicircle CDE on the bottom, minus the area of semicircle ABC on top.

Answer: D
Solution:
All the units digits of the product (2*4*6*8) *(2*4*6*8)…. =384*384*…=384^10, 4^1=4; 4^2=16; 4^3=64, So, the units digit of 384^10 is 6.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,